This post is about the Critical Speed Map (CSM), one of the most important evaluation criteria for rotor dynamics in turbomachinery. A critical speed map can provide significant insights into the potential behavior of a rotor-bearing system without requiring extensive model details.
DyRoBeS software can help explore how a CSM can be a useful design tool. Our simple example model consists of a shaft, two bearings near the ends of the shaft, and three disks mounted near the center of the shaft.

Figure 1: DyRoBeS Model
At this point, the only details we need about the bearings are the bore diameters and the locations of their centerlines. We don’t need to worry about bearing design details or the type of bearings used. Additionally, the effects of forces on seals, impellers, etc., can be neglected.
The undamped critical speed map is essentially a parametric study of how the undamped critical speeds of a rotor-bearing system change with bearing stiffness. For our example system, let’s assume the bearings have relatively low stiffness: 10,000 lb/in. The following figures show the frequencies and mode shapes associated with the first three critical speeds:
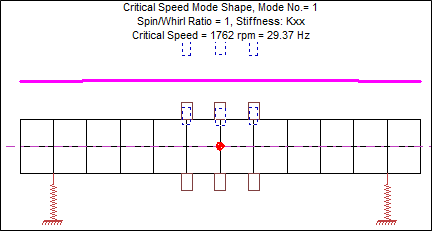
Figure 2: 1st Critical Speed, Kxx=Kyy=10,000 lb/in
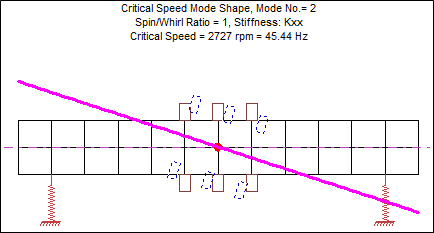
Figure 3: 2nd Critical Speed, Kxx=Kyy=10,000 lb/in
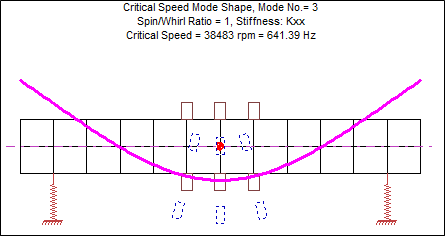
Figure 4: 3rd Critical Speed, Kxx=Kyy=10,000 lb/in
Looking at the mode shapes for the first two critical speeds, we see the shaft moving as a nearly rigid body. For these two critical speeds, almost all deflection occurs in the bearings. For the third critical speed, the shaft takes on a bending shape. What happens if we make the bearings stiffer? Let’s reconstruct the critical speed mode shapes using a bearing stiffness of 500,000 lb/in.
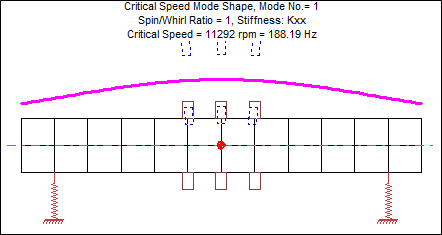
Figure 5: 1st Critical Speed, Kxx=Kyy=500,000 lb/in
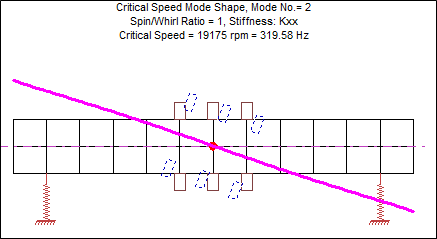
Figure 6: 2nd Critical Speed, Kxx=Kyy=500,000 lb/in
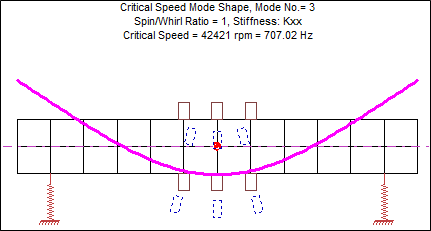
Figure 7: 3rd Critical Speed, Kxx=Kyy=500,000 lb/in
With this increased bearing stiffness, the first critical speed increased by 6.4 times (from 1,762 rpm to 11,292 rpm), and the second critical speed increased by 7 times (from 2,727 rpm to 19,175 rpm). In contrast, the third critical speed changed very little (from 38,483 rpm to 42,421 rpm). When creating a critical speed map, we can see how the critical speeds change over a wide range of bearing stiffness.

Figure 8: Critical Speed Map
The critical speed map shows that black dots correspond to the first example (Kxx=Kyy=10,000 lb/in), and blue dots correspond to the second example (Kxx=Kyy=500,000 lb/in). Sloping lines in the CSM for the first two critical speeds indicate significant deflections at the bearing locations. However, the third critical speed appears as a horizontal line, showing minimal sensitivity to bearing stiffness. If bearing stiffness is very high, all three critical speeds appear as horizontal lines in the CSM.
For our example, let’s assume the machine must operate continuously in the speed range of 8,000 rpm to 12,000 rpm. We can add this speed range to the CSM using horizontal dashed lines.
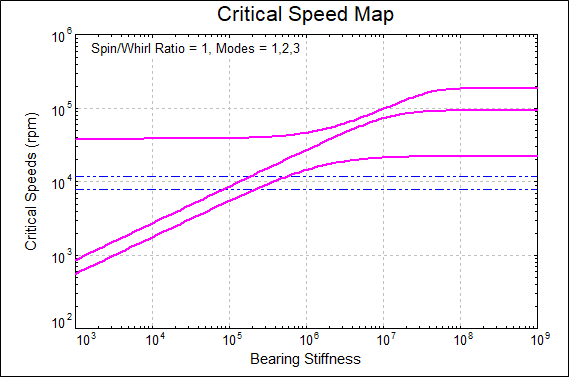
Figure 9: Critical Speed Map with Operating Speed Lines
This CSM shows that if the actual bearing stiffness is below approximately 75,000 lb/in, the first two critical speeds will fall below the continuous operating speed, and the machine will only pass through them during startup. If the bearing stiffness were around 200,000 lb/in, the first critical speed would fall near the lower end of the operating range, and the second near the upper end.
It’s worth noting that this simple analysis doesn’t include the effects of damping or how critical speeds might actually be excited during operation. However, we can conclude that an undamped critical speed map provides valuable insights in the early stages of rotor dynamics analysis.



